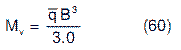Los sistemas estructurales que usualmente se cimientan en zapatas continuas o “corridas” son los pórticos y la mampostería estructural.
En general, Si el área requerida para la cimentación es mayor del 30% pero menor del 50 % del área de la planta del edificio o estructura, se puede pensar en una viga continua como posible sistema de cimentación.
El algoritmo de la metodología tradicional para calcular una viga de fundación en un edificio de mampostería, asumiendo una distribución uniforme de presiones debajo de la zapata igual a la capacidad admisible del suelo qa ,es el siguiente:
1 Se determina el ancho de la viga:
2 Se determina el peralte de la viga. Como una aproximación empírica para calcular la altura de la viga de fundación, se recomienda considerar 10 cm por cada piso, esto es:
3 Se calcula la cortante unidireccional (se hace por metro lineal)
Donde f = 0.85
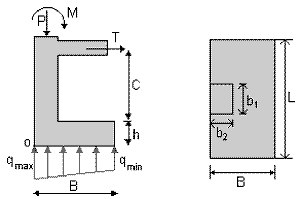
4 Se calcula el momento. Se utiliza la sección crítica indicada en la Figura 28
FIGURA 28. Sección crítica para el cálculo del momento en zapata continua.
En el sentido longitudinal de la viga, el acero de refuerzo que se coloca es el mínimo, dado por la expresión 0.0018 B d
La aplicación de este algoritmo produce resultados aceptables cuando se trata de cimentar sistemas de mampostería estructural (muros reforzados), donde el asentamiento, como se verá más adelante, no depende de la rigidez de la fundación, sino de la rigidez de los muros del edificio y en donde no se justifica un estudio profundo de Interacción Suelo Estructura (ISE).
Una edificación puede ser concebida de modo que los muros estructurales se apoyen en un sistema o entramado de vigas continuas en dos direcciones, tal como se ilustra en la Figura 29. Este sistema se caracteriza por su alta hiperestaticidad y rigidez (deseable). En este caso las rigieses deberán ser
aproximadamente iguales en ambas direcciones.
FIGURA 29. Alternativa de cimentación consistente en un sistema o entramado de zapatas continuas en dos direcciones.
Los sistemas estructurales aporticado y de mampostería estructural apoyados en vigas continuas fueron estudiados por Wilson de J. Herrón Durán (9). En este trabajo se sistematizaron los algoritmos del método interacción suelo – estructura, en el PROGRAMA DE INTERACCIÓN SUELO – ESTRUCTURA Versión 2.0, utilidad que facilitó la comparación con los métodos clásicos de análisis y permitió la observación del comportamiento de las estructuras en función de las más importantes variables que intervienen en el problema: compresibilidad del suelo (mv), rigidez de la zapata, rigidez y configuración de la superestructura.
Con respecto al estudio de los sistemas aporticados apoyados en zapatas continuas, Herrón Durán presenta importantes conclusiones, algunas de las cuales se relacionan a continuación:
· Para el cálculo de los elementos mecánicos (fuerza axial, momento y cortante) de la zapata continua, cuando ésta sirve de cimentación a un pórtico, la precisión en la compresibilidad del suelo (módulo de compresibilidad mv), no es determinante. En efecto, cuando la variación de la compresibilidad en el estrato inmediatamente debajo de la cimentación es aproximadamente un 50%, el diagrama de momentos permanece prácticamente igual para fines ingenieriles. Cuando la variación de mv es mucho mayor (del orden de 1000%), el momento sufre una variación considerable, evento en el cual es mejor optar por una cimentación más económica: la zapata aislada.
· Los asentamientos total y diferencial de la estructura si varían en forma directa con la variación de la compresibilidad.
· El aumento de la rigidez de la zapata continua implica un aumento en el diagrama de momentos y simultáneamente un mayor control de los asentamientos diferenciales.
· El aporte de rigidez que hace la superestructura a la cimentación es muy poca. En la mayoría de los casos es despreciable, ya que el resultado obtenido al analizar la viga de cimentación sin tener en cuenta la rigidez de la superestructura es igual, para efectos de diseño, al obtenido cuando se considera toda la estructura.
· No es conveniente utilizar el método tradicional que parte de la suposición de reacción uniforme y lineal, ya que casi siempre este método aumenta los valores de los momentos, haciendo más costoso el diseño, o los subestima, haciéndolo inseguro.
· Cuanto mayor sea el número de luces que presente un pórtico apoyado en zapata continua, mayor será la justificación para realizar un análisis ISE.
· Cuanto mayor sea la separación de las columnas de un pórtico apoyado en zapata continua, mayor será la justificación para realizar un análisis ISE.
· Los resultados de la ISE son más coherentes con el comportamiento físico suelo – estructura que cualquier otro método tradicional, proporcionando generalmente un diseño más económico y seguro.
Las conclusiones más relevantes con respecto al estudio de sistemas de muros estructurales apoyados en zapatas continuas, presentadas por Herrón Durán son:
· La cimentación de una mampostería estructural sin vanos (garaje, pasadizo, etc) debe proveer la rigidez suficiente para impedir que el muro absorba las solicitaciones inducidas por asentamientos diferenciales. Esto se logra proporcionando un peralte importante a la sección y una cuantía mínima de acero de refuerzo.
· Se recomienda (y este es un aporte innovador de Herrón – Garza), para la zapata continua que sirve de cimentación a una mampostería con vanos (garaje, pasadizo, etc), no apoyarla en la zona donde el muro no le trasmite carga, tal y como se ilustra en la Figura 30. Este modelo controla mucho mejor los asentamientos diferenciales y rebaja considerablemente el diagrama de momentos en un porcentaje que puede llegar a ser del 500%, según sea la carga que transmite el muro y la longitud del hueco, pudiéndose entonces utilizar zapatas más flexibles y eficientes.
FIGURA 30. Detalle donde se indica la interrupción del apoyo en una zapata
continua cuando se presentan vanos en la mampostería.
· La variación de la rigidez de la zapata continua que sirve de cimiento a una mampostería estructural, en la mayoría de los casos, no varía sustancialmente el régimen de momentos. Es posible trabajar con la rigidez mínima exigida por la Norma, puesto que da asentamientos diferenciales tolerables.
· La influencia de la compresibilidad del estrato en los elementos mecánicos de la estructura de cimentación es muy poca, casi despreciable. Esta variable afecta en forma casi directa el valor del asentamiento total.
Estas conclusiones del trabajo de Herrón Durán (9) fueron posteriormente verificadas y ratificadas por Juan Carlos Botero Martínez y Juan Carlos Gómez Zuluaga (0).