Un diseño de zapata medianera siguiendo el modelo descrito en el numeral anterior, concibe la viga aérea trabajando a una determinada tensión T que garantiza una distribución uniforme de presiones q.
A continuación se explicará una alternativa de diseño que se ajusta a los resultados obtenidos con un análisis de interacción suelo – estructura (ISE) la cual considera que la acción del momento trata de volcar la zapata, produciendo como efecto una reacción lineal no uniforme, con mayor intensidad de presiones en el vértice “o” de la zapata (Figura 19).
A diferencia del modelo con distribución uniforme de presiones, presentado en el numeral anterior, donde el número de ecuaciones son suficientes para despejar la incógnita del problema T, en este caso, dado que las incógnitas son tres (T, qmax y qmin ) y el número de ecuaciones son dos

el problema no tiene solución directa, es preciso entonces recurrir a una ecuación de compatibilidad de deformaciones, utilizando para su deducción la Figura 20.
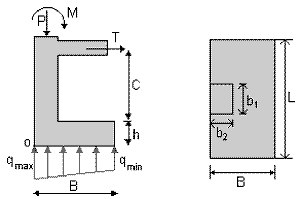
Figura 19. Modelo estructural de la zapata medianera con distribución variable de presiones con viga aérea, presentada por José Calavera.
Figura 20. Modelo del giro y del asentamiento en zapata medianera con viga aérea presentado por José Calavera.
En estas expresiones, K representa el módulo de reacción del suelo, conocido también como módulo de balasto.
De otro lado, utilizando la fórmula para calcular la deformación de un voladizo con carga concentrada en el extremo T, se deduce para el cálculo del giro de la columna la siguiente expresión:
En estas expresiones, K representa el módulo de reacción del suelo, conocido también como módulo de balasto.
De otro lado, utilizando la fórmula para calcular la deformación de un voladizo con carga concentrada en el extremo T, se deduce para el cálculo del giro de la columna la siguiente expresión:
Igualando los giros de la zapata y de la columna, se obtiene una de las tres ecuaciones que permite resolver el problema:
Con respecto a la ecuación (45), es importante observar que:
· A mayor brazo de palanca (valor de C), menor será el valor de T.
· Si el sentido del momento M es antihorario, es decir, hacia afuera, tratando de abrir las columnas, mayor será el valor de T.
· Debido a que los resultados obtenidos mediante la aplicación de esta expresión son inferiores a los obtenidos mediante un análisis de Interacción suelo estructura, se recomienda, para el cálculo del acero de refuerzo de la viga, duplicar este valor.
El valor del coeficiente de balasto K está dado por la expresión:
En esta última expresión, el término ES representa el módulo de elasticidad del suelo, que se expresa en kg/cm2 y es igual al inverso del módulo de compresibilidad volumétrica mv, el cual se determina mediante el ensayo de consolidación. Por consiguiente, se puede escribir:
El término m representa la relación de Poisson del suelo de fundación; su valor es de 0.35 para suelos arcillosos y de 0.25 para arenas.
En la aplicación del sistema de ecuaciones (45), (46) y (47), se presentan en la práctica dos casos para el análisis: En el primero, se fijan las dimensiones de la zapata B, L y h y con el valor del coeficiente de balasto K, el cual se debe conocer previamente, se obtienen, mediante la solución del sistema de ecuaciones, las
tensiones qmax y qmin y la fuerza T.
En el segundo caso, fijando las presiones qmax y qmin y la altura total de la zapata h, se determinan las dimensiones B y L de la zapata, mediante tanteos.
Para la determinación de las dimensiones de la zapata medianera con viga aérea se recomienda una relación de forma L/B igual a 2, pues ésta optimiza la cuantía total de refuerzo en ambas direcciones de la placas de este tipo de cimentación.











0 comentarios:
Publicar un comentario