Se estudiará en este curso el caso de zapatas esquineras con dos vigas aéreas, considerando que bajo la cimentación existe una distribución de presiones linealmente variable, presentando para este propósito el fundamento teórico expuesto por José Calavera en su referencia (5).
José Calavera presenta un análisis partiendo del hecho de que la complejidad del modelo es muy grande si la columna y la zapata no son cuadrados. Puesto que en el caso de zapatas de esquina no existe ninguna restricción preferente para hacerlas mayores en una dirección que en la otra, en lo que sigue, el método se expondrá para el caso de zapata cuadrada.
FIGURA 21. Geometría del modelo estructural de la zapata esquinera con dos vigas aéreas presentado por José Calavera.
En la Figura 21 se muestra el esquema estructural y las fuerzas en equilibrio.
En la Figura 22 se muestra una sección transversal trazada justo por la diagonal de la zapata, con base en la cual se determinan las ecuaciones de equilibrio suponiendo que todo el terreno bajo la zapata está comprimido.
FIGURA 22. Modelo estructural de la zapata esquinera con distribución variable de presiones y dos vigas aéreas.
La tercera ecuación necesaria para resolver el problema es obtenida de la compatibilidad de deformaciones, igualando el giro de la zapata al de la columna, suponiendo un módulo de balasto K:
De la solución del sistema de ecuaciones (52), (53) y (54) resultan las expresiones necesarias para resolver el problema:
En el segundo caso, se fijan las tensiones qmax y qmin y se estima el valor de K, lo cual equivale a estimar las dimensiones del cimiento, y esto puede también requerir algún tanteo.
En la Figura 23 se representa el comportamiento de la zapata esquinera frente a los momentos que sobre ella actúan.
Calavera (5) supone que la placa (zapata) está apoyada sobre dos vigas virtuales en voladizo. Otros autores han encontrado que la placa está sometida a dos momentos máximos, uno (MT) en dirección de la diagonal que pasa por la columna y que produce tracciones en la cara superior de la zapata (Figura 23 (b)), y otro (ML) en dirección ortogonal a la anterior, que produce tracciones en la cara inferior (Figura 23 (c)). La magnitud de estos momentos es prácticamente la misma, siendo por unidad de ancho igual a:
FIGURA 23. Momentos que actúan sobre la zapata esquinera.
Para el refuerzo en el centro de la placa (Figura 24 a) se colocan dos parrillas
arriba y abajo de modo que cada una resista ML = MT. El diseño de las vigas virtuales se realiza para el momento:
En las expresiones (59) y (60) q representa la presión promedia bajo la zapata, es decir:
FIGURA 24. Distribución del acero de refuerzo en la zapata esquinera.








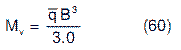



0 comentarios:
Publicar un comentario